The Vastness of Space
To quote from HitchHiker's Guide to the Galaxy and one of my own publications that I wrote for kids" “Space is big. Space is really big! You just would not believe how vastly hugely mind-bogglingly big it is."
He was not kidding either! Imagine it this way. Pretend you are on the Autobahn in Germany. You are in a Ferrari, zooming at 300 kph (186 mph). If you did not have to stop, you could go around the earth in about 133 hours, or 5 and a half days. Now imagine if your Ferrari suddenly could travel to the sun. It would take nearly 4,000 times longer to get to the sun than to drive around the earth! That is ~22,000 days in the Ferrari! The closest star that is not the sun is called Alpha Centauri, The closest star to our solar system. It is 1.37 parsecs, or 41.53 trillion kilometers, from Earth. To get there, it would be like driving to the sun almost 300,000 times! The closest galaxy, Andromeda, is nearly 600,000 times farther than Alpha Centauri! The farthest galaxies I measure are over 100 times farther than Andromeda, and to get to the end of the visible universe, you have to go almost 150 times farther than that! Anyway, if you wanted to drive to the end of the visible universe, or pretty much anywhere out in space, it would take a really long time."
Now, that's pretty big. So big in fact that no human could truly comprehend it's size.
Ok, but how do we even know this? Like seriously, no one has a measuring tape that extends to distant space objects.
No one has ever been to Alpha Centauri and seriously, It's hard enough just trying to go to the moon!
If you approach the distance problem at the right angle, you'll see that the answer is geometry. More specifically triangles and all of their angles as the three angles within a triangle will generally always add up to 180 degrees.
Triangles are also very stiff, meaning that for 3 given side lengths, you always have to have 3 corresponding side lengths.
Because of this, if you know just the right combination of sides and angles of a triangle, you can figure out the rest of the triangle.
The whole goal to measure how far away everything is and as such, Astronomers when they distance things abuse the crap out of the fact that triangles are so consistent.
Measuring the distance to the Sun
We know the distance to the sun using even more geometry, planets, and the moon. We also know that the Earth orbits along the sun.
There is a very nice diagram from the ask an astronomer website that is hosted by Cornell. Basically, it shows that we can construct a diagram between the sun, Venus and the Earth. This diagram happens to be a triangle. The first thing you need to do to get one of the angles of the triangle is by finding the 'greatest point of elongation'
| The key to figuring out how far away the sun is, is by finding the 'greatest point of elongation'. You do this when you observe Venus going in front of the sun (like the moon in a lunar eclipse) and constantly measuring the growing angle in the sky Venus makes with the sun. Once that angle stops growing and begins shrinking, you have found your angle. You can read more about how this diagram is constructed here. If you are interested, you can go onto ask an astronomer yourself and your question could be answered! |
This 'greatest point of elongation' happens when a planet like Venus transits across the sun. After it transits it will appear to travel away from the sun, stop, and then go closer to the sun.
The greatest point of elongation for a Venus Solar eclipse is the point after the eclipse which Venus stops appearing to move away from the sun and begins to appear to move towards the sun.
Triangles, Parallax, and Stars
We then use something called parallax. My very first YouTube Video I posted on my Youtube channel specifically explains parallax (Or at least I try, man I feel so cringe whenever I look at my own stuff)!
Using parallax and the distance of the earth from the sun, we can construct another triangle (astronomers love triangles!). NASA has a very good diagram which shows off a stellar parallax triangle.
 |
| This shows what parallax is. By measuring how much a star appears to move in the sky (how much the sky angle changes), as the earth orbits the sun, compared to stars that are extremely far away (and therefore don't appear to move at all), we can construct a triangle where we know the angles and the length of one side, which is enough to measure a distance. Image Credit: NASA/ESA, A.Feild/STScI |
Since we know how big one of the sides of the triangle is (the distance of the earth from the sun), and since we can measure the angle a star moves in the sky as the earth orbits the sun, we can then construct the triangle we need to measure the distance to a star.
Astronomers tried to make doing all the math easier by defining a parsec, parsecs being related to arc seconds. Basically, the sky rotates above us by one arc second every second (an arc minute is 60 arc seconds, and arc hour is 60 arm minutes). The sky rotates 360 degrees every 24 arc hours (60x60x24 arc seconds), which is one day, in sync with the clock.
Finally a Parsec is defined by if that star shifts around 2 arc second in the sky over the course of a whole year. It is 2 arc seconds because that is what we decided it should be (also right triangles are even more fun).
Using triangles and the distance to the sun, we know that 1 arc second of parallax is around 31 trillion kilometers or 19.2 trillion miles (Holy smokes!).
Knowing all this we can measure the Orion system, otherwise known as Orion's Belt, to be nearly 12 quadrillion kilometers (around 7 quadrillion miles) distant from Earth!
 |
| The three brightest stars going across the diagonal of the image is Orion's Belt. Basically if you watch this star throughout the year you will see it move around. A paper published in 2013 measured a parallax of around 0.0026 arc seconds, which if you do 1/0.0026 you get 384 parsecs. Since we know the distance of one Parsec using geometry, we calculate the Orion's belt star system to be nearly 12 quadrillion kilometers (around 7 quadrillion miles) from earth! Credit: Davide De Martin & the ESA/ESO/NASA Photoshop FITS Liberator |
What Astronomers do When Triangles Start Failing
At some point, stars can get so far away, that they appear to be completely motionless on the sky when using the earth's orbit with parallax. To get further than what Earth allows, we have launched space craft like Gaia to get even better measurements of parallax. Eventually though, even Gaia cannot tell whether a star is changing position since the angles just get so tiny, usually around 10000 ish parsecs.
We then have to use a distance that is measured using something called a "standard candle". A standard candle is a star (or object) in space where the brightness is intrinsic, or that we know how much total light that object is creating. When you increase your distance from that object, you see less and less light from that object. In fact, the amount of light you recieve is proportional to your distance from the object squared.
 |
| These photos describe why standard candles give the distance to an object. The photo on the left is if you were close to a campfire, you could feel its heat and possibly read a book. On the right, the fire is still visible but dimmer, because it is farther away. If you know how much light the fire is creating when close to it, you will know how far away you are from the fire based upon how dim it looks as you walk away. Photo on the left can be found here. The photo on the right can be found here |
What this means is that if you are next to a campfire and are receiving 100 watts of light energy (similar to a 100 watt lightbulb) is
- If you walked to 2 meters away you would be receiving 25 watts/m^2 of light energy (100w / (2mx2m) = 25).
- If you walked 5 meters away, you would be receiving 4 watts/m^2 of light energy (100w/ (5x5) = 4).
- If you walked 10 meters, you be getting only 1 watts/m^2 of light energy (100w/ (10x10) = 1).
A watt is a unit of power, or how much light you are getting, while m stand for meter. W/m^2 tells you how much light you are getting in a certain amount of Area.
Cepheid variable stars are a good example of a standard candle. The reason why is that Cepheids have this cool trait where their brightness goes up and down over a period of time, while also being predictably the same brightness from star to star.
If you were to measure how much light energy you get from a Cepheid overtime the graph would look something like this
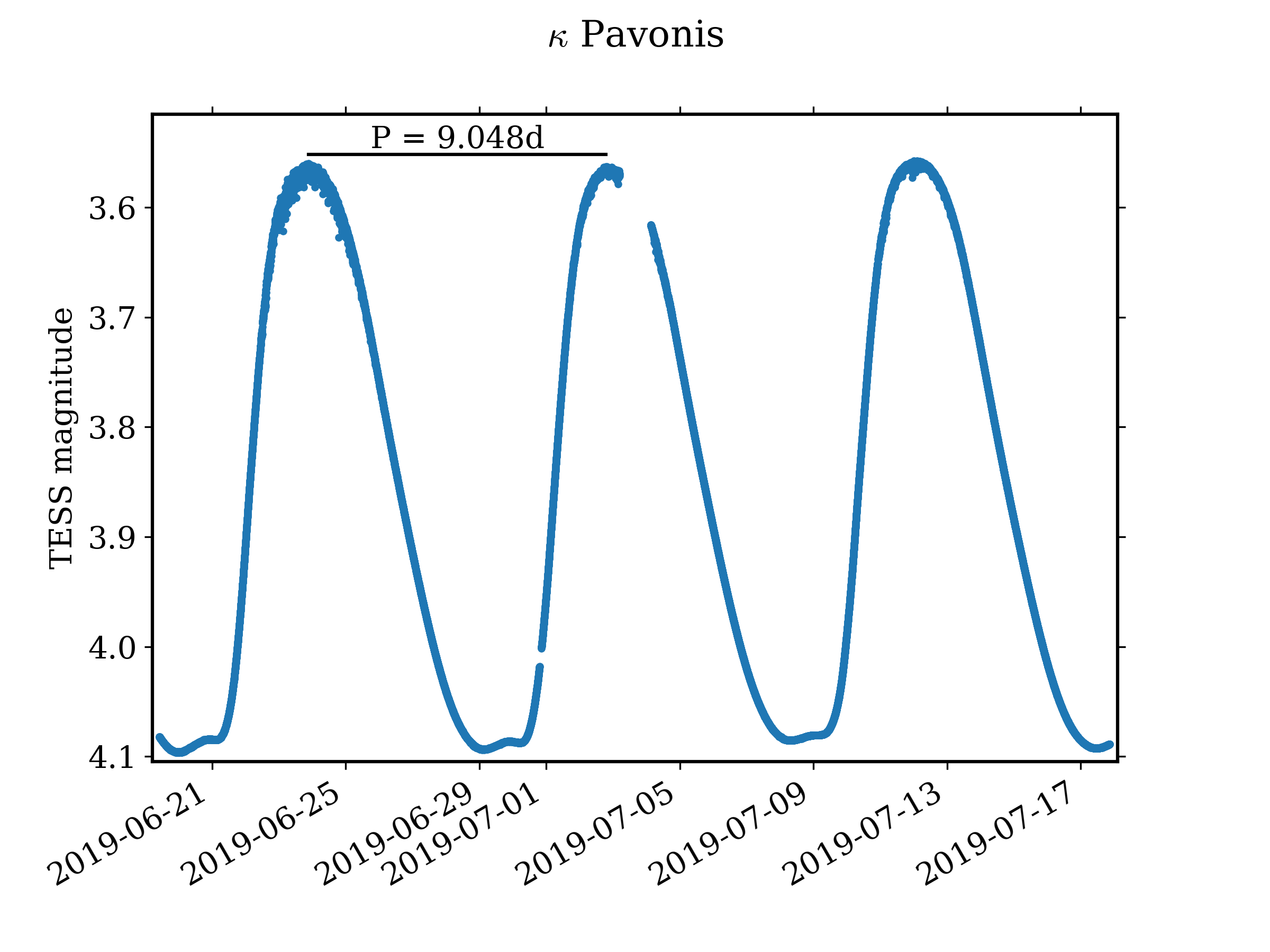 |
| The amount of light a Cepheid give off overtime. You can see that it gets brighter, then dimmer, then brighter over and over again. If we can then identify what type of Cepheid star it is, we will know how much light it is creating. If we know how much light it is creating, we can finally measure how far away the star is! Warrick Ball - Lightcurve of the W Virginis (Type II Cepheid) variable κ Pavonis recorded by NASA's Transiting Exoplanet Survey Satellite (TESS). |
I know a graph isn't super exciting, but the periodic dimming and brightening is exactly what we look for! In order for it to be identified as a Cepheid the light curve must have this periodic dimming and brightening.
Brightness from Cepheids are very consistent from one Cepheid to the next, the brightness being related to how long the dimming and brightening cycle is. Now, as we know that all Cepheids are mostly the same in brightness, if we find a Cepheid that is close to earth, close enough to use parallax to measure a distance, we can compare the light from the Cepheid we know the distance to, to other Cepheids where we don't know the distance, just like with the fire.
- We start by measuring one Cepheid that give us 100 power units that we know using geometry is 100 parsecs away (1,000,000/(100*100) = 100) .
- By measuring another similar Cepheid that gives us 1 power unit, we know that it must be 1,000 parsecs away (1,000,000/(1000*1000) = 1).
- If we measure another similar Cepheid giving us 1/100 of a power unit, we know that it must be 10,000 parsecs away (1,000,000/(10000*10000) = 1/100)
- If we measure another similar Cepheid giving us 1/10000 of a power unit, we know that it must be 100,000 parsecs away (1,000,000/(100000*100000) = 1/10000)
It is basically the exact same logic as with the fire example, but in reverse. Also, I use power units instead of Watts because 100 watts would be WAY too high than what is realistic. This technique with Cepheids can go all to way to millions of parsecs, which includes other galaxies, which is quite a jump from previous geometrical methods.
Can we go farther?
Yes we can, but we have reached the end of the line as far as stars go.
Or have we?
There is indeed one more very important distance tool when it comes to stars, but that will have to wait for another blog.
Regardless, if you want to measure the distance to a far off star, you first need a love of triangles. Once you have your love with triangles solidified, you then need to measure as many angles as you can, including some very special angles.
You can then look for Cepheids using a really fancy camera, calibrate your camera to a Cepheid you can measure a distance to that Cepheid using triangles with angle measurements. Finally, you can start measuring ultra distant galaxy Cepheids using your calibration Cepheid.
Of course, measuring distances does get a bit more complicated in practice, but hopefully I was able to convey the basic gist of what is going on.
Space is a big place and it is hard to imagine just how mind bogglingly big it is. However, the way we measure distances is based off of verifiable geometry, trigonometry, and how light travels through space. Even though it can be difficult to comprehend, geometry confirms that space really is incomprehensibly vast.
Comments
Post a Comment