We all know and love the sun (hopefully anyway). It's the brightest thing in the sky from our perspective here on earth. The Sun provides all the energy necessary for things to live on earth. Without the Sun's power, the only things that would be left, are maybe some very exotic forms of bacteria and ocean life that rely on hydrothermal vents on the bottom of the ocean.
 |
| An incredibly photo of the sun provided by the European Space Agency's Solar Orbiter. Without this brilliantly hot and extremely stable star, life on Earth as we know it would be entirely impossible. You can read more about it here. Credit: Solar Orbiter/EUI Team/ ESA & NASA; CSL, IAS, MPS, PMOD/WRC, ROB, UCL/MSSL |
How The Sun Creates Energy
The sun is extremely stable and is currently in the phase known as the main sequence stage. Stars undergo this phase as a part of their life cycle. We call it the main sequence stage since this is the main Hydrogen burning phase of our Sun's life cycle.
To explain further, many stars (including our sun) start as a collapsing cloud of gas and dust, with most of the collapsing stuff being Hydrogen. At a certain point, due to the immense pressure caused by gravity and super high temperature caused by increased pressure, Hydrogen will begin to fuse into Helium. A basic way to think about fusion is simply 4 Hydrogen atoms being forced together (through a long chain of events)
 |
| An illustration of a possible chain of events that can happen in the Fusion cycle of Hydrogen within a star. You start out with 4 Hydrogen atoms, and end up with a single Helium 4 atom Image can be found here |
This process of fusing Hydrogen into Helium is a process that produces a lot of energy, in the form of heat and light. In fact, Einstein himself helped figure out why fusion produces energy with his famous equation
 |
| Einstein's famous equation. This equation states that energy is equivlant to a given amount of mass, multnbniplied by the speed of light squared. It will be very useful for calcuating how much Hydrogen the sun is fusing. I got this equation from Google search. |
Using Einstein to Calculate How much Energy Fusion Produces
We know that Hydrogen has an atomic weight of 1.00784. We know that Helium 4 atoms have an atomic weight of 4.002603254. By considering the sun to be only fusing Hydrogen into Helium in order to produce it's energy, we can find exactly how much energy the sun is producing through a short calculation.
- 100 x (1-(4.002603254 / (4 x 1.00784))) = 0.71333%
This shows that when you fuse 4 Hydrogen atoms into 1 Helium atoms, the resulting Helium atom is actually lighter than the original 4 Hydrogen atoms by about 1%. Conservation of mass says that mass had to go somewhere as it just can't disappear. Using Einstein's equation, we can deduce that energy is equivalent to mass.
Using Einstein's equation, if we measure all the energy that this process generated, we find that it is equivalent to the amount of mass that we lost! In other words, using the fusion process, mass is converted into heat and light energy.
The Logic Behind Calculating how Much Hydrogen is being Fused within the Sun
Now you might think it would be super complicated to figure out exactly how much Hydrogen the sun is fusing. However, if we get clever, it's actually not too difficult (maybe just involves a couple of steps), as the key thing we know is that the sun is in equilibrium. Being in equilibrium means that the sun does not release more energy than it produces.
Assume the Sun Is in Equilibrium
We also know that when things get hot, they tend to want to expand. The Ideal gas law is a good example of this. It is also partly why when you cook something and put it in some tupperware (or a can/jar) while it is still hot, it will form a seal and will suck in air when you open it again, as when the food cools down, the gas inside (and the food a tiny bit) takes up slightly less space.
The nuclear fusion process is dependent upon pressure and temperature. The sun has a somewhat analogous behavior to a gas (but definitely not exactly the same) in that the hotter the core gets, the bigger the Sun will become. If solar fusion in the sun's core produces more heat and light energy than is being released by the sun surface, it will start to grow in size and release more energy. If solar fusion produces less energy than is being released at the sun's surface, the sun will start to shrink and release less energy.
Since the size of the sun seems to be pretty stable, that must mean that the amount of energy being produced by solar fusion in the core is about the same as the total amount of energy being released. In other words, the energy produced is in equilibrium with the energy being released. If this wasn't the case, then the sun should be changing more dramatically, which it doesn't seem to be doing. The sun isn't in perfect equilibrium as it does seem to be changing somewhat overtime, but for this purpose I will assume that it does indeed remain constant.
Using this, all we need to know is how big the sun is, the temperature of the sun. You can measure the temperature of the sun using a cool device called a pyrometer. You can also measure the Sun's temperature by using a Spectrometer. A Spectrometer gives you how much light you are getting at different wavelengths of light (with different wavelengths of light can corresponding to different colors of light). By measuring the Sun's spectrum, finding the maximum wavelength, or 'light color', that the Sun is producing, and than using Wien's law
 |
| Wien's law equation which I got from google search. If you measure the solar spectrum and find the maximum wavelength of light, you can get the temperature. It turns out that the peak wavelength of the sun is around 500 nanometers, which corresponds to green light, which if you plug in the numbers gives a temperature of 5772 Kelvin. You can read more about Wien's law here. |
we can calculate the temperature of the Sun, which turns out to be around 5772 Kelvin (which is around 6000 Celsius, or 10000 Fahrenheit. I will use Kelvin because it makes my life easier). You can find out how big the sun is by using the surface area of a sphere equation, along with some geometry to measure the distance and the radius, something I discuss somewhat in measuring distances to stars.
Use The Luminosity Equation to get Energy Output of the Sun
Once you have the surface area and temperature you can use the Luminosity Equation
 |
| The Luminosity equation which can be used to calculate how much energy the sun (and other stars) is releasing. The Stefan-Boltzmann constant is just a constant multiplier that always remains the same, no matter what type of star you are looking at. I got this from google search by searching for "Luminosity Equation". You can find more information about the luminosity equation here |
Using Wien's Law, we know the sun is about 5772 Kelvin. Using geometry we know the radius of the sun to be about 695,700,000 meters which can be used to get the surface area 4 x Pi x Radius^2. Finally, with the Luminosity equation and the Stefan-Boltzmann constant, by plugging all of these numbers we can finally get the answer of 4x10^26 Watts (that a 4 with 26 zeros after it) for the total energy out of the Sun!
Calculating how Much Hydrogen is being Fused
As discussed previously, we can use Einstein's equation an energy conservation
E = mc^2
and simply plug in the value 4x10^26 Watts that we obtained from the Luminosity equation for the energy E. Now all we need to do is divide by the speed of light squared (divide by the speed of light twice) in order to get the amount of mass which needs to be converted to energy. This gives
mass = 4x10^26 Watts / (speed of light x speed of light) = 4.451 x 10^9 kilograms per second
Meaning that in order for the Sun to maintain the energy output it has, it must be converting nearly 4.5 billion kilograms of mass into pure energy every single second.
Since fusing Hydrogen will only turn 0.71333% of the mass into energy, as we calculated earlier, to get the final amount of Hydrogen the sun must fuse per second to maintain the solar output we see, we get
4.451 x 10^9 kilograms per second / 0.0071333 = 6.24 x 10^11 kg/s
Meaning the sun fuses nearly one trillion kilograms of Hydrogen every single second into Helium in order to maintain it's current energy production.
What Will The Future of the Sun look like
Eventually the sun is theorized to turn into a red giant. This happens when the sun starts to run out of Hydrogen to fuse and begins to fuse more Helium with Hydrogen. The various processes behind why can get somewhat in depth, but in short, in order for Helium to fuse, higher temperatures are needed. We discussed earlier that the sun is in equilibrium. If the temperature of the core of the sun increases, that means that the equilibrium size of the sun will expand. The Sun will begin to grow in size, and possibly get so large as to swallow the earth. I even did a short YouTube animation going over some of this
A Final Calculation of How Long the Sun Has Before the Red Giant Phase
We can get a rough estimate of how much time it will take for the sun to become a red giant. Taking some facts we know about the sun, that it has a mas of 2 x 10^30 kg, about 70% of that mass is Hydrogen, we assume that the core only has access to about 10 % of the Hydrogen to fuse (only hydrogen in the core will be able to fuse) before moving onto the Red Giant phase (which could dramatically increase fusion speeds), we can do a quick calculation
Time to red Giant Phase = (0.07 x 2x10^30 kg / 6.24 x 10^11 kg/s) = 1.122x10^18 seconds
1.122x10^18 seconds is around 7 billion years. If we take a look at a diagram of the life cycle of the sun found on a NASA website
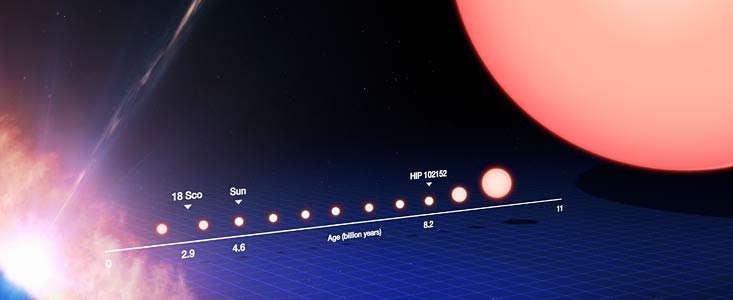 |
| A illustrative depiction of the life cycle of the sun. I retrieved it from a NASA website here. You can find out even more details about this diagram and the life cycle of the sun here, which is where I originally found the diagram. Credit: ESO/M. Kornmesser |
We find that our rough calculation with our simplifying assumptions didn't do too shabby. Other typical answers of how long the sun still has left in it's main phase are around the 5 billion range. Sadly, regardless of exactly how long the sun will live is not a question anyone of us will ever be able to fully answer, since we will all be long dead before it ever happens. There still seems to be plenty of Hydrogen left to burn, and a human's lifespan is insignificant to the time span of the cosmos.
These calculations simplified much, but hopefully it gives some clarity over why we think the way we do about the Sun's eventual evolution into a red giant.
I looiive this article.
ReplyDelete